Survey of the stable marriage problem
In 2012, the Nobel Prize in Economic Sciences was awarded to Alvin Roth and Lloyd Shapley for their work on designing practical market systems. At the heart of this recognition was a deceptively simple mathematical problem known as the Stable Marriage Problem, which has become a key player in matching processes that shape our daily lives—from job placements to college admissions and organ transplants.
The Stable Marriage Problem was first introduced in a 1962 paper by David Gale and Lloyd Shapley, who proposed a straightforward algorithm to solve the following theoretical conundrum: Suppose there are \(n\) men and \(n\) women who are eager to be married. Each participant has strictly ranked all the members of the opposite gender in the order of their preference. Suppose a matchmaker matches the men and women. Now, if a man and a woman find that they prefer each other over their partners, they have a great incentive to break their marriages and choose each other. Such a situation is undesirable because we expect marriages to be stable. So we wonder
Can we always marry the men and women off so that no two people prefer each other over their matched partners?
Note that “stable match” is a property of all the marriages and not a property of an individual couple. This is so because stability depends on the options outside the marriage.
Let us begin with an example: Suppose Anthara (A), Bhavana (B), and Chaitra (C) will be matched with advith (a), balaji (b), and charan (c). We will denote their preference list :
| advith | balaji | charan | |
|---|---|---|---|
| Anthara | a,B | c,A | b,A |
| Bhavana | c,A | a,B | b,B |
| Chaithra | a,C | b,C | c,C |
The preference list of women is read along the rows and for the men it is along the columns. For instance, Bhavana prefers charan over advith and advith over balaji. An example of a stable marriage would be the following pairing advith marries Bhavana, balaji marries Chaithra and charan marries Anthara. We will denote this stable match by {aB,bC,cA}.
Gale and Shapely (1967) proved that a stable match exists no matter the preference lists of the participants. They even proposed an algorithm to find a stable match! In their algorithm, men propose to women in rounds. Women can only lock (temporarily accept) or reject men each round. A locked man can only propose once he is rejected. At any point, proposed women will have locked in one man. Let us take a quick look at their “deferred acceptance” algorithm:
- In the first round, the men propose to the highest-ranked women on their list. The women may receive multiple proposals or none at all. If they receive multiple proposals, each woman chooses the most preferred man available and tells him that she is considering his proposal (thereby locking him). She rejects the other men.
- In the next round, the rejected men propose to their next preferred woman. At this point, only if any woman gets a more preferred man will she reject the one she is considering. Now, she considers the more preferred man (thereby locks him).
- The rounds continue, with rejected men proposing to the most preferred among the remaining women and women locking/rejecting according to the previous bullet point. The algorithm terminates when men have no new women to propose to. Finally, women marry the men they are considering. By the end of the algorithm, every woman would be proposed, and thus, all participants could be paired off. Gale and Shapely proved that the marriage found by the described algorithm will always be stable.
If there are multiple stable marriages, how does one compare them? In our example, M1={aB,bC,cA} and M2={aA,bC,cB} are stable matches. The stable marriage {aB,bC,cA} is better for men (called men-optimal-stable-matching or MOSM) since they get more preferred partners than {aA,bC,cB}. But for women, it is the opposite. Among two stable marriages $M_1, M_2$ we say \(M_1 \leq M_2\) if, for every man, the wife assigned in $M_2$ is not preferred less than the one in \(M_1\). Gale and Shapely showed that their algorithm will always find the marriage that is the best possible match for men (the proposers), which is also the worst possible for the women (the proposed) for the order \(\leq\).
In a standard economics setup, the stability of prices is an indicator of the efficient allocation of resources to participants. But in markets like residency programs for doctors or college admissions for students, we are interested in efficient allocation across two different kinds of participants without prices! Economists can rejoice since the algorithm provides an efficient allocation (i.e. a stable match). Furthermore, computer scientists can rejoice since the algorithm terminates at a maximum of \(n^2-2n+2\) rounds. So, we have a polynomial time algorithm (meaning fast algorithm) to find the marriages.
Conway discovered that the collection of all stable marriages, with the order \(\leq\) discussed above, forms a beautiful mathematical object called a “distributive lattice”. This is discussed in Knuth’s lucid exposition. Irving and Leather used the distributive lattice structure to show that listing all possible, stable marriages is a hard computer science problem. Blair proved a converse to Conway’s observation. He revealed that every finite distributive lattice is a set of stable marriages.
Knuth added a stochastic angle to the problem by assuming that preference lists are chosen randomly and n is large (asymptotic analysis). In the described algorithm, if a man has made $k$ proposals by the end, he will marry the woman ranked \(k\) in his list. So, the average number of proposals is also the average wife rank. Knuth/Prescott showed that the average number of proposals is roughly \(n \ln n\) and thus, the average wife’s rank is roughly \(\ln n\) . The same analysis shows the average husband’s rank is \(\frac{n}{\ln n}\). Note that if you put \(n=3000\), then the average wife rank is 8 and average husband rank is 375. Low husband rank is not surprising considering that Gale-Shapely algorithm always finds the worst matches for women, even on average we expect it to be bad.
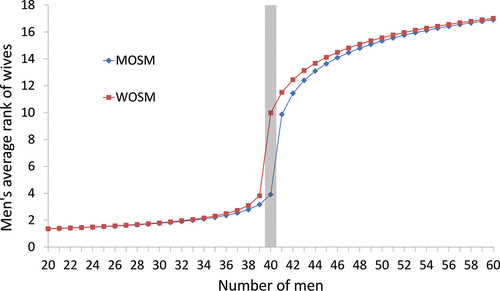
Interestingly, in 2017, Ashlagi et al showed that if the matching problem was between n+1 men and n women, the average husband rank is $\ln n$ and the average wife rank is \(\frac{n}{\ln n}\) (i.e. the rank situation flips!). This shows that there is extreme competition in matching markets. If men propose then we denote the situation by man-optimal-stable-matching (MOSM) and if women propose we denote the situation by WOSM. In a setting with 40 women, and n men, the figure shows the average wife rank has a sharp jump when the number of men cross 40 irrespective of who is doing the proposing. So the shorter side of the market gets one of their top choices with very high probability. The remarkable effect of a single additional man is the following: while the unmatched man is willing to be matched with any woman, he creates a useful outside option only for a few women who rank him favorably. However, this outside option makes these women better off, making their spouses worse off. The women who like these spouses must, in turn, be made better off. This effect ripples through the entire market, making most women better off.
The fact that proposed (women) get least preferred matches among all stable marriages is good motivation for them to lie about their preferences. So the natural question is whether women can gain a better outcome by lying about their preferences. The answer is yes! . In our example, if Anthara decides to lie about her preferences and announces that she prefers a>b>c (instead of her real preference a>c>b), then the Gale-Shapely algorithm will produce the match M2 which is women-optimal. On the other hand, Roth shows that in any procedure which produces optimal results for one side, truthful revelation of preferences is a dominant strategy (for men in Gale-Shapely algorithm for instance). The incentive to misrepresent preferences motivates the model of a non-cooperative game where the strategy set of participants is the collection of possible preference lists they might state. Roth proved that if the agents misstate their preferences optimally with respect to each other, i.e. their (mis)stated preferences form a Nash equilibrium, then an algorithm like Gale-Shapely’s will yield stable outcomes in terms of their agents true preferences. If the Gale-Shapely algorithm is used, Roth showed that men have no incentive to lie.
The structural simplicity of the stable marriage problem belies its immense practical utility. Variants like the residency matching market, organ donor markets, high school admissions market are studied seriously today. Roth seriously studied the problem motivated by the residency matching problem. The National Residency Matching Program (NRMP) in the U.S. was forced to change tactics because the algorithm could be manipulated by the proposed through misstating their preferences. In 1984 they changed their system to applicant proposing from hospital proposing. The existence of stable solutions, speed of the matching algorithm, the potential for games and the competitiveness of the stable matching market continues to enthral mathematicians, economists, and computer scientists.